

| Moebius, a modeling system for mathematics and science |
|
|
Models easy build and simulate In today's world, predictions based on model calculations are becoming increasingly important. Growth processes occur in a similar way in the social and natural sciences. With simple models, one can conclude how a growth process will proceed. It is therefore important that students are introduced to such models and their limitations at an early age. The math. methods are simple and can be dealt with in mathematics lessons. In subjects where mathematics is not to be the main focus, semantic models or graphic illustrations of relationships are used. Apart from formulating the model, an important learning objective is the evaluation and interpretation of the model calculation in graphs and tables.Modeling systems are tools that allow the user to perform model calculations and to display the results in graphs or tables. |
|
Graph: Simulation of the thyroid control circuit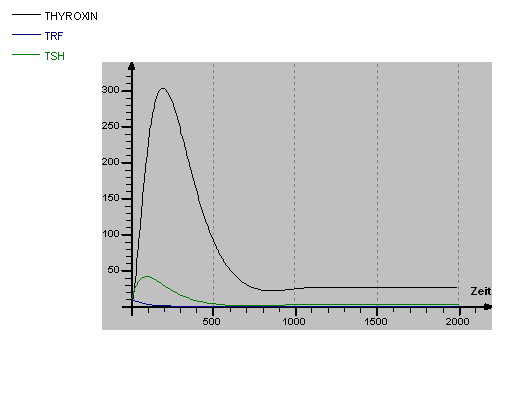 |
|
| Moebius was developed under the point of view to create models that are as simple and transparent as possible. Thereby we consciously focused on complicated math. procedure was renounced. Some specialists will miss the Runge-Kutta method. But it cannot be the purpose of school lessons to use such university procedures as black box methods. Rather, the chance should be taken to use the simple procedures in order to obtain nonsensical results and thus to show the limits of the computer. On the other hand, a misunderstood method that eliminates these errors leads to unreflected computer credulity. | |
Graphical model: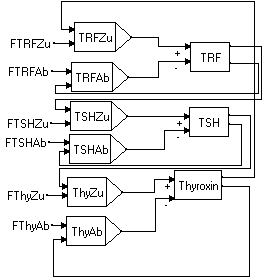 |
The mathematician should also not stop at the linguistic or graphical formulation of the problems, but use the translation into a formula language, which is one of the elementary goals of mathematics teaching. Therefore Moebius has three types of modeling: Semantic models (the more the more..) Graphic models Algorithmic models |
| Moebius always translates a sematic or graphic model into a program, the algorithmic model. So the actual calculation does not remain hidden. The physicist, who usually already formulates his models in formulas, will dispense with the first two types and start immediately with the algorithmic method. |
Algorithmic model of a capacitor discharge: U:=Q/C I:=U/R DeltaQ:=I*DeltaT Q:=Q-DeltaQ t:=t+DeltaT |

