

| Moebius, ein
Modellbildungssystem für Mathematik und Naturwissenschaften |
|
|
ZIP-Datei mit allen Simulationen zur Schrödingergleichung herunterladen.(1MB) Lösung der Schrödingergleichung mit Moebius Hat man mit den Schülern z.B. die Schwingungsdifferentialgleichung schon mit Moebius gelöst, dann ergeben sich hier keine neuen Probleme. Man löst die Schrödingergleichung, indem man in kleinen Schritten jeweils annimmt, dass die zweite bzw. erste Ableitung konstant ist. Programm für den Potentialtopf: | |
| if x<=L then V=5 | Links ist der Topf 5 eV hoch |
| if x>=L then V=0 | im Topf ist das Potential 0 |
| if x>=R then V=5 | Rechts ist der Topf 5eV hoch |
| psi2:=-C*(E-V)*psi | Schrödingergleichung, E Energie des Teilches, V Potential |
| psi1:=psi1+psi2*dx | Berechnung der ersten Ableitung |
| psi:=psi+psi1*dx | Berechnung von psi |
| x:=x+dx | Fortschritt von x |
| p:=psi*psi | Wahrscheinlichkeitsfunktion |
Ergebnis: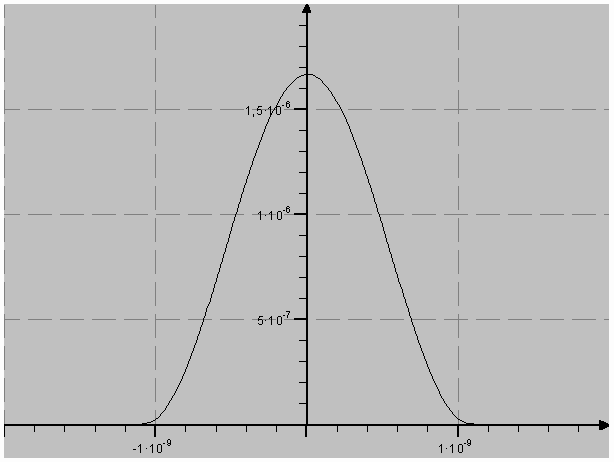
|
|
| Beim Coulombpotential ergibt sich zusätzlich folgendes Problem. Das Potential ist kugelsymmetrisch. Für die Berechnung der Antreffwahrscheinlichkeit muss man beachten, dass Oberfläche einer Kugelschale proportional zu r2 ist. Wir rechnen eindimensional und erhalten damit die Antreffwahrscheinlichkeit auf einer solchen Kugeloberfläche. Das bedeutet, die berechnete Wahrscheinlichkeit muss durch r2 geteilt werden, um die Wahrscheinlichkeit am Ort x,y,z zu erhalten. | |
|
Programm für das Coulombpotential | |
| V:=-k/x | Coulomb-Potential |
| psi2:=-C*(E-V)*psi | Schrödingergleichung, E Energie des Teilchens, V Potential |
| psi1:=psi1+psi2*dx | Berechnung der ersten Ableitung |
| psi:=psi+psi1*dx | Berechnung von psi |
| x:=x+dx | Fortschritt von x |
| p:=psi*psi/x/x | Wahrscheinlichkeitsfunktion |
Ergebnis: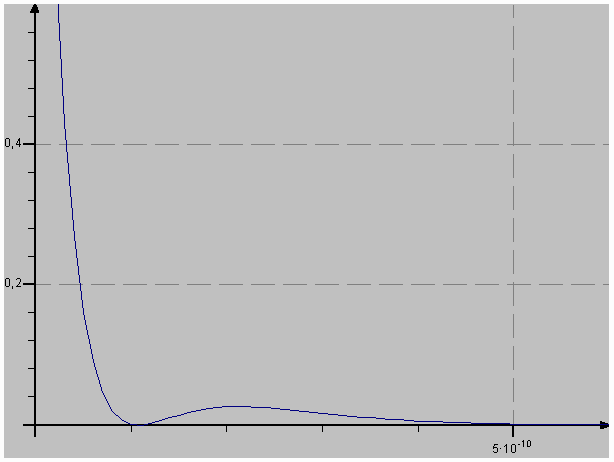 |
|
| Zeigt man dieses
eindimensionale Ergebnis dreidimensional an, dann erhält man
die kugelsymmetrischen Antreffwahrscheinlichkeiten. |
|
|
3D-Programm für Coulombpotential V:=-k/r if alpha=0 then psi2:= -C*(E-V)*psi;psi1:=psi1+psi2*dr;psi:=psi+psi1*dr x:=r*cos(alpha);y:=r*sin(alpha) alpha:=alpha+dalpha; if r >0,85e-10 then dr := 8e-12 if alpha>6,28 then alpha:=0;r:=r+dr;p:=psi*psi/r/r |
|
Ein Ergebnis (je nach Startwert): |
|
Aktuell: Simulation einer Corona-Pandemie mit Moebius
Die neue IPhone/IPad-Version oder Mac-Version können Sie aus dem Apple App Store herunterladen.
Klicken Sie auf das Logo, um in den Apple App Store zu wechseln.

Hier erfahren Sie mehr über Schullizenzen bei Apple.
Klicken Sie auf das Logo, um in den Apple App Store zu wechseln.

Hier erfahren Sie mehr über Schullizenzen bei Apple.
Die Windows-Version von Moebius ist im Microsoft App Store erhältlich.
Klicken Sie auf das Logo, um in den Microsoft App Store zu wechseln.

Wenn Sie früher eine Schullizenz für Moebius erworben haben, dann können Sie hier einen Download-Link zu der älteren Version anfordern.
Download-Link anfordern
Schülerinnen und Schüler können hier eine kostenlose Version für zu Hause herunterladen. Diese darf nicht im Unterricht eingesetzt werden!
Der Freistaat Sachsen hat eine Landeslizenz für das Programm Moebius erworben: Diese erlaubt die Installation der Moebius-Software auf allen Computern der allgemeinbildenden Gymnasien, Abendgymnasien, Kollegs, der beruflichen Gymnasien und Fachoberschulen des Freistaats Sachsen, des Sächsischen Bildungsinstituts, der Sächsischen Bildungsagentur und des Sächsischen Staatsministeriums für Kultus. Schulen aus anderen Bundesländern sind nicht berechtigt diese Programmversion zu verwenden. Klicken Sie hier, wenn Sie berechtigt sind, diese Version herunterzuladen.
Klicken Sie auf das Logo, um in den Microsoft App Store zu wechseln.

Wenn Sie früher eine Schullizenz für Moebius erworben haben, dann können Sie hier einen Download-Link zu der älteren Version anfordern.
Download-Link anfordern
Schülerinnen und Schüler können hier eine kostenlose Version für zu Hause herunterladen. Diese darf nicht im Unterricht eingesetzt werden!
Der Freistaat Sachsen hat eine Landeslizenz für das Programm Moebius erworben: Diese erlaubt die Installation der Moebius-Software auf allen Computern der allgemeinbildenden Gymnasien, Abendgymnasien, Kollegs, der beruflichen Gymnasien und Fachoberschulen des Freistaats Sachsen, des Sächsischen Bildungsinstituts, der Sächsischen Bildungsagentur und des Sächsischen Staatsministeriums für Kultus. Schulen aus anderen Bundesländern sind nicht berechtigt diese Programmversion zu verwenden. Klicken Sie hier, wenn Sie berechtigt sind, diese Version herunterzuladen.
